Back-propagation explained
反向传导算法的本质是用链式法则求复合函数的导数,其数学基础就是复合函数的链式法则求导:
对函数
因此,一个简洁的推导应该将所有的层都抽象成成一个函数,而不去区分卷积层、全连接层和激活函数的特殊情况。 只要这个函数数值可导,那么在反向传导中就遵循相同的数学规则。 在神经网络中,这样一个函数又被称作“operator”。
在这篇文章里,我们试图根据链式法则,对网络所有类型的层(operator)用统一的形式解释清楚链式法则和反向传导算法。 相比之前的一些解释,这一套解释数学上非常清晰,涉及的数学符号非常少: 在前向传导时,每层只有输入
前向传导 Forward Pass
这部分没什么好讲的,为了引出数学符号的定义简单介绍一下。 如果对这部分比较熟悉,建议直接跳到 反向传导 部分。
对于一个神经网络,
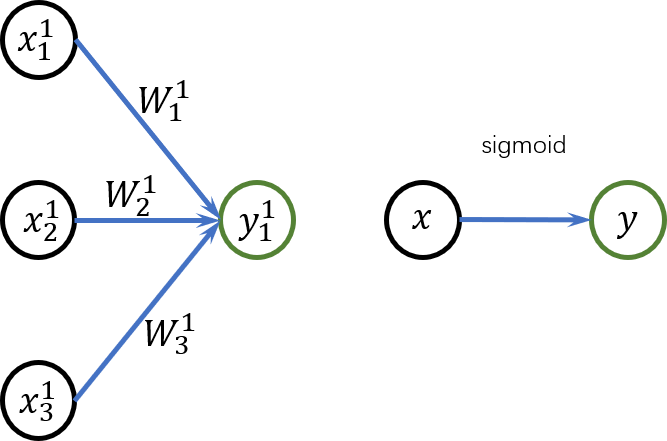
一个简单的线性操作(卷积) 和非线性操作 (sigmoid函数)。 左:
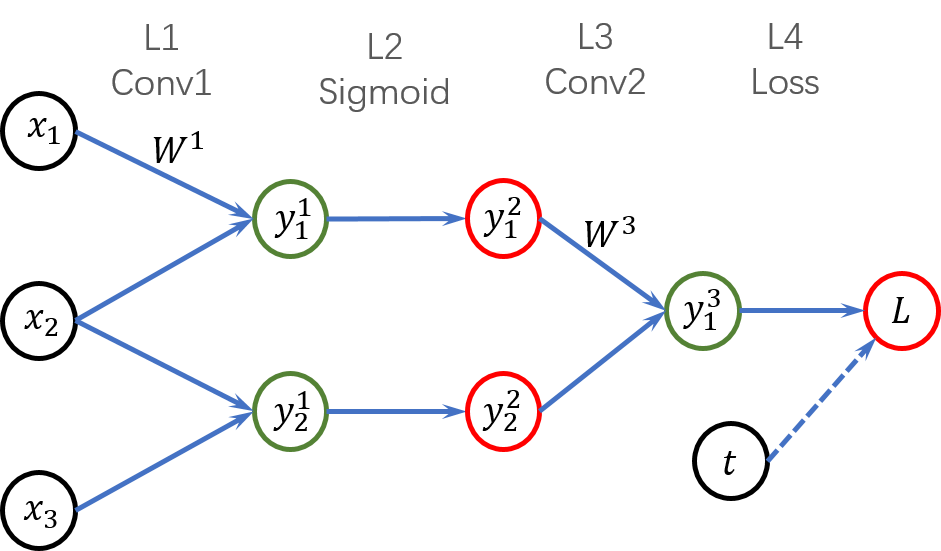
一个简单的三层网络,每一个箭头的连接都对应一个权重(为了简便,每层的权重只用一个数学符号标注)。
最后一层接受两个输入(第 3 层的输出
上图是一个简单的 4 层神经网络,输入数据依次通过“卷积”
反向传导 Back Propagation
假设神经网络第
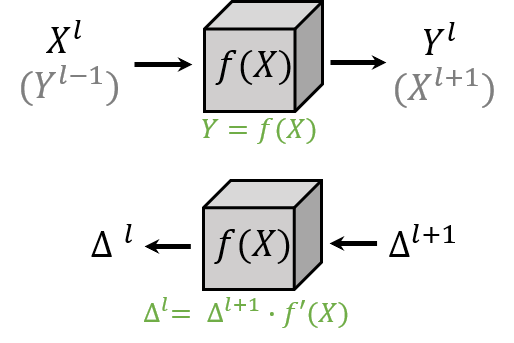
把网络的一层当做一个黑盒子,前向传导的时候输入
我们把
因为
这里我们不像其他的各种文章中分别把激活函数、损失函数当做特殊条件。在反向传导中,梯度传播的规则就只有 Eq.
- 如果
- 如果
下面我分别用激活函数、卷积层、全连接层和损失函数作为示例,说明这几种 operator 的反向传播规则看似各不一样, 其实都遵循 Eq.
激活函数的反向传导
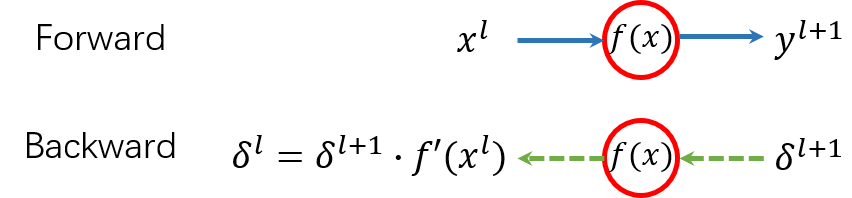
激活函数的前向传导和反向传导。在反向传导时,输入后一层的梯度
由于激活函数都是单输入单输出的,我们可以用数值符号(而非向量)描述激活函数的反向传导过程。 假设激活函数是
Sigmoid 和 ReLU 反向传导,以及为什么 ReLU 可以进行 inplace 前向传导
这里我们列举化两个比较典型的激活函数:Sigmoid 和 ReLU。 首先写出这两个激活函数的函数式:
结合 Eq.
观察 Eq.
实际上 Sigmoid 函数的输入
卷积层/全连接层的反向传导
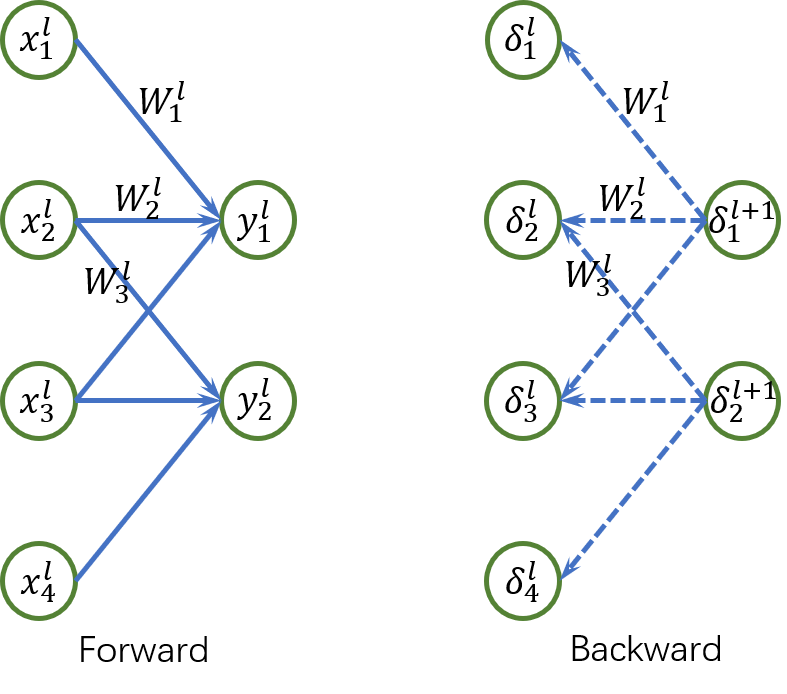
卷积层和全连接层的反向传导法则:后一层的梯度
在全连接层和卷积层中,前层的梯度等于后层梯度沿连接的权重回传。 也即在上图中,
结合 Eq.
池化层层的反向传导
相比卷积/全连接层,池化层的反向传导就更简单了,因为池化操作本身可以看作输入
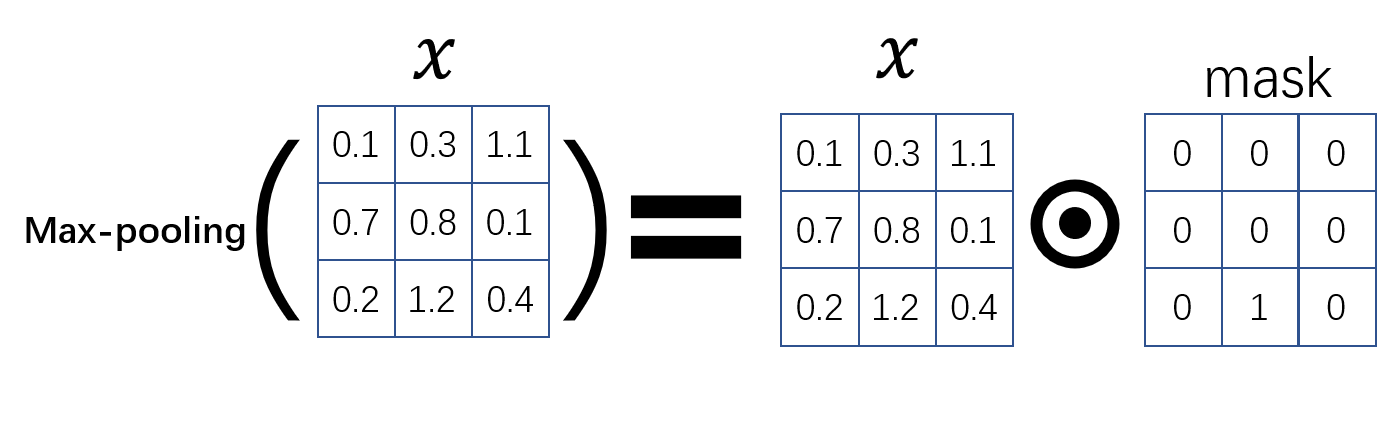
Max-pooling 等价于输入
因此,对于 max-pooling 而言,其反向传导规则为:
损失函数的反向传导
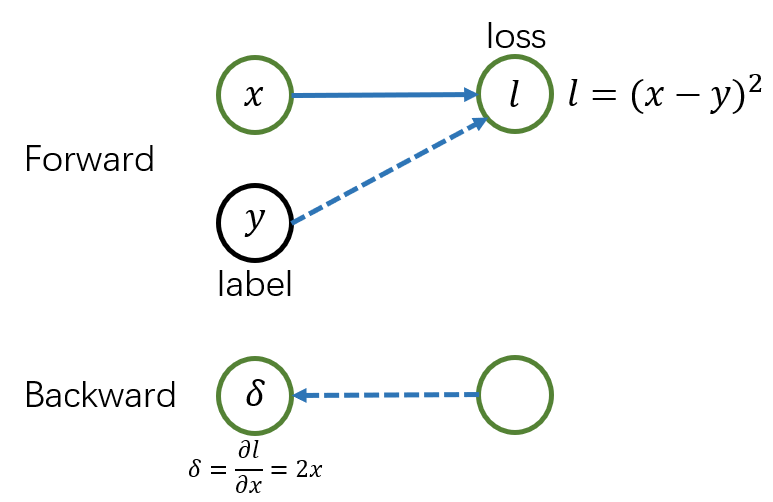
平方损失函数
损失函数是神经网络的最后一层,因此不用接收后层传回来的梯度。损失函数在反向传导时直接计算损失
损失函数对各层参数
经过前面的梯度反传,我们得到了最后的损失
卷积层中对权重
我们以一个简单的卷积层为例,可以用很简单的推导得出损失函数对权重

如上图所示,经过反向传导,损失函数
因为
卷积层中对偏置
考虑卷积中的偏置项:
至此,我们得到了损失函数对权重
用 PyTorch 验证全连接层的反向传导规则:
下面我们在 pytorch 中用一个
import torch.nn as nn
linear = nn.Linear(4, 2)
linear.weight.data.fill_(1)
linear.bias.data.fill_(0)
x = torch.ones(1, 4)
x.requires_grad = True
y = linear(x)
y.retain_grad()
loss = (y**2).sum()
loss.backward()
print("y = ", y)
print("y_grad = ", y.grad)
print("w_grad = ", linear.weight.grad)
由于
y = tensor([[4., 4.]], grad_fn=)
y_grad = tensor([[8., 8.]])
w_grad = tensor([[8., 8., 8., 8.],
[8., 8., 8., 8.]])
总结 Conclusion remarks
总的来说,反向传导算法从将数据
- 前向传导,得到各层的输出
- 从损失函数开始由后向前,根据 Eq.
- 根据 Eq.
补充阅读
- Overview of PyTorch Autograd Engine.
- https://www.cs.toronto.edu/~rgrosse/courses/csc321_2018/slides/lec10.pdf.
全文完,感谢阅读。如果你有任何问题,或者发现有任何表述、数学表达的错误,请在下方留言。
title = {Back-propagation Explained},
author = {Kai Zhao},
year = 2016,
note = {\url{http://kaizhao.net/posts/bp}}
}